
Newton and Leibnitz are both credited with inventing calculus around the turn of the 18th century. A lay person might think that these geniuses both wrote a 300 page math textbook on the subject to gain fame -- wrong! They had the key ideas regarding rate of change (differentiation) and its opposite (integration). The ideas were so powerful that physicists, astronomers, and engineers started to use the new math to solve the pressing problems of the day. Everyone was happy except ensuing mathematicians who introduced functions and series that the undeveloped calculus could not address.
The Advanced Calculus course I just completed used the book "
A Radical Approach to Real Analysis" to teach the foundations of calculus from an historical perspective. The book cites the work of Fourier, Cauchy, Abel, and Dirichlet (there were certainly others) as the 19th century mathematicians who laid the rigorous foundation for calculus so that strange new functions like the one below could be analyzed.
I perceived two central tools used for the area of mathematics called real analysis (sometimes called "the "epsilon/delta" game or "epsilonics") -- the Mean Value Theorem and Uniform Convergence Theorems. Every student of calculus should remember the Mean Value Theorem:
Let y = f(x) be a function with the following two properties: f(x) is continuous on the closed interval [a,b]; and f(x) is differentiable on the open interval (a,b). Then there exists at least one point c in the open interval (a,b) such that:

This is an incredibly powerful theorem that can be used to prove numerous results. Here's something I had to prove as a homework assignment:

The notion of Uniform Convergence and the theorems related to it really gave mathematicians a handle on functions defined as the sum of infinite series of functions (e.g. Fourier series). This topic is a little too complex to discuss here except to summarize that a function having the property of uniform convergence can be integrated term by term and potentially differentiated term by term (for this the sum of derivatives must also be uniformly convergent).
Generally if a function is not uniformly convergent it fails at some troublesome point. Consider the function:
 on the interval [0,1]. If you take enough terms (increase the value of N) this function behaves like the zero function, f(x) = 0, for all points in the interval [0,1] except at 0. Here the function "blows up" as shown in this plot:
on the interval [0,1]. If you take enough terms (increase the value of N) this function behaves like the zero function, f(x) = 0, for all points in the interval [0,1] except at 0. Here the function "blows up" as shown in this plot:
Simply put the function is not convergent at x = 0 (see the big hump just to the left of .2).
All of this analysis helped put calculus on a rigorous footing going into the 20th century and enabled the production of the calculus tomes (mine is almost 900 pages!) from which many of us studied. So even though calc students distain epsilon/delta arguments and the like, I salute the pioneers of calculus. Hail to Fourier, Cauchy, Abel, and Dirichlet!


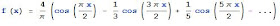
 This is an incredibly powerful theorem that can be used to prove numerous results. Here's something I had to prove as a homework assignment:
This is an incredibly powerful theorem that can be used to prove numerous results. Here's something I had to prove as a homework assignment: The notion of Uniform Convergence and the theorems related to it really gave mathematicians a handle on functions defined as the sum of infinite series of functions (e.g. Fourier series). This topic is a little too complex to discuss here except to summarize that a function having the property of uniform convergence can be integrated term by term and potentially differentiated term by term (for this the sum of derivatives must also be uniformly convergent).
The notion of Uniform Convergence and the theorems related to it really gave mathematicians a handle on functions defined as the sum of infinite series of functions (e.g. Fourier series). This topic is a little too complex to discuss here except to summarize that a function having the property of uniform convergence can be integrated term by term and potentially differentiated term by term (for this the sum of derivatives must also be uniformly convergent). on the interval [0,1]. If you take enough terms (increase the value of N) this function behaves like the zero function, f(x) = 0, for all points in the interval [0,1] except at 0. Here the function "blows up" as shown in this plot:
on the interval [0,1]. If you take enough terms (increase the value of N) this function behaves like the zero function, f(x) = 0, for all points in the interval [0,1] except at 0. Here the function "blows up" as shown in this plot: