Complex Numbers: More Real Than You Imagine

My last course was titled Complex Analysis where we studied functions f(z) of complex variables z = x+ i*y. We methodically defined complex versions of familiar functions like sine, cosine, exp, and the like, and then studied their properties including differentiation and integration. If this sounds boring, it’s not. For example, we have Euler’s Identity ⅇ^ⅈπ=-1 which relates four of the primary constants of mathematics. The identity follows directly from Euler’s definition of ⅇ^ⅈθ=cosθ+ⅈsinθ to which he was led so that familiar properties like ⅇ^(x1+x2)=ⅇ^(x1)×ⅇ^(x2) worked for complex numbers as they did for reals.

Now what’s particularly fascinating about Complex Analysis is that is can be used to prove all kinds of results involving real variables. Let’s define the norm of a complex number as x + i y = (x^2 +y^2)^1/2 . There’s a property of complex numbers that says

Use this to define the multiplication of the sum of squares of two real numbers in terms of complex numbers (“≡” means “is defined as”). Example:
Here we have a result from number theory that states that the product of a sum of two squares is itself the sum of two squares. This is always true, although somewhat surprising to see the ease with which the calculation proceeds using complex numbers.Okay, you’re not impressed. How about the proof of the Fundamental Theorem of Algebra which states that if

is a non-constant polynomial of degree ≥ 1 with complex coefficients, then the equation

has a root in .
This theorem is impossible to prove using the real number system; however, with complex numbers it’s almost a one liner when you employ Liouville’s Theorem.

Another very strange phenomenon has to do with real integrals like:

This result cannot be derived by standard calculus. Instead it is a fall-out of the Cauchy Integral Theorem (CIT) and Cauchy Integral Formula (CIF). To get this result you have to find the right contour in the complex plane and perform complex integration on its boundary. One part of the contour will be the x-axis giving the real-valued integral on the left. The complex integrals are computed using either CIT or CIF and when the results are combined out pops a real number!

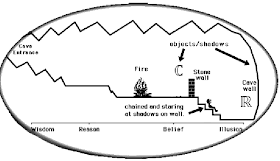
To really appreciate these wonders you must take the course. My wonderment leads me to a mathematical version Plato’s allegory of the cave. In The Math Cave the real numbers are the shadows that we see and take for reality. However, in truth, the complex numbers are the source of the shadows.