Is There Anything as Simple/Complex as a Group?

My summer 2009 session course was Group Theory. What is a group?

A group is an ordered pair (G, ·) such that G is a set, · is an associative binary operator on G, and $ e Î G such that:

1. If a Î G the a · e =a,
   


2. If a Î G, then $ a^-1
   Î G such that a · a^-1 = e.
   

What could be simpler? A group is a set of objects and some kind of operation that has straightforward properties. Groups are all around us and come in all shapes (2D, 3D) and sizes (finite, infinite). Examples of finite groups are:
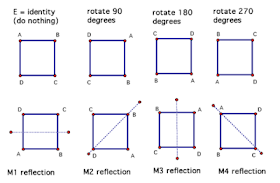
1) the symmetries of a square and rotations through various axes and
2) the set {0,1,2,3,4,5,6,7} with modulo 8 addition.

Examples of infinite groups are:
3) the set of integers and addition
4) the set of rational numbers – {0} and multiplication.

Okay we have sets of objects with an interesting behavior. Can we find any more of them? Well how about taking a subset of them and seeing if they are also interesting. Viola, consider the subgroup.

A subgroup of a group G is a subset which is a group under the operation in G. More precisely, a subgroup of a group (G, ·) is a group (H, *) such that H is a subset of G and * is the restriction of · to H x H. This means that multiplication is the same in H as it is in G.

Looking for subgroups in the examples above:
1) the horizontal and vertical rotations of a square is a subgroup of all the symmetries
2) {0,2,4,6} with modulo 8 addition is a subgroup of Z₈ above
3) the set of multiples of 3 is a subgroup of integers and addition
4) the set of rational numbers with even denominators – {0} is a subgroup.

Really simple stuff, right? Well let's define two terms, a theorem, another term, and another theorem and reconsider.

Definition: The normalizer of N(S) of S in G is defined by N(S) = {x Î G xS = Sx}.

Definition: If S and S' are subsets of group G, then S is conjugate to S' iff
$ x Î G such that S' = x^-1 S x.

Theorem: Conjugacy is an equivalence relations.

Definition: The conjugate class on a subset S of a group G is the set Cl(S) of subsets S' of G which are conjugate to S.

Theorem: If S is a subset of a group G then [G:N(S)] = o(Cl(S)).

Oh no, now we're in the deep end of the pool and we don't know how to swim. This is typical of Group Theory (and higher math in general). Define something that's pretty simple and prove some stuff about it. Then define a new abstraction on top of that and prove some more theorems. Then define
some more stuff on top of THAT... You get the picture.

In this manner group theory leads to these kinds of groups: cyclic, abelian, free, solvable, divisible, decomposable, p-groups, supersolvable, M groups, etc. How can something so simple now be so complex?

P.S. the text was "Group Theory" by W. R. Scott which I would avoid like the plaque. It has very, very few examples and I think examples are needed to wrap your head around all of the abstractions being thrown at you.